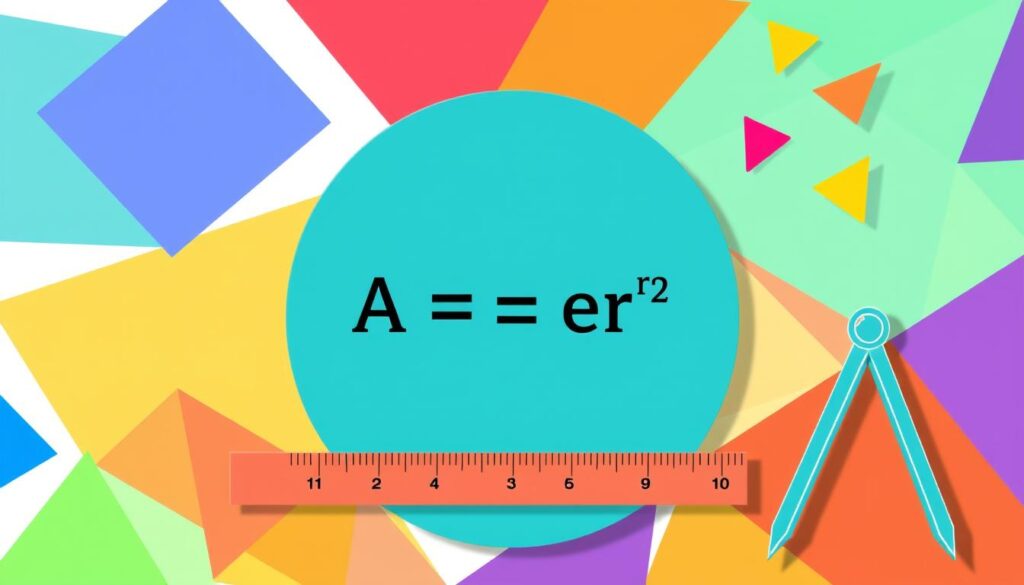Obliczanie pola okręgu jest prostsze niż mogłoby się wydawać. To kluczowa umiejętność w geometria okręguPole to przestrzeń wewnątrz okręgu mierzona w jednostkach kwadratowych.1.
Okręgi mają specjalne cechy, które sprawiają, że obliczenia powierzchni są precyzyjne. Każdy okrąg ma punkt środkowy i promień. Promień biegnie od środka do krawędzi1.
Ten wzór na pole koła jest A = πr². To równanie wykorzystuje promień okręgu do znalezienia pola1. Pi (π) jest tutaj kluczowe i zwykle zaokrągla się je do 3,142.
Najważniejsze wnioski
- Pole koła mierzy się w jednostkach kwadratowych
- Wzór A = πr² jest podstawą do obliczania pola koła
- Zrozumienie promienia i pi (π) jest kluczowe
- Pole koła można obliczyć za pomocą promienia, średnicy lub obwodu
- Dokładne obliczenia zależą od dokładnych pomiarów
Zrozumienie koła i jego składników
Okręgi to urzekające kształty, które można znaleźć wszędzie w naszym codziennym życiu. Te idealnie zakrzywione formy mają wyjątkowe właściwości, które czynią je kluczowymi w wielu dziedzinach3.
Definiowanie podstawowych elementów okręgu
Okrąg to kształt, w którym każdy punkt krawędzi jest równo oddalony od środka. Przyjrzyjmy się jego kluczowym częściom:
- Promień: Odległość od środka do dowolnego punktu na krawędzi okręgu.4
- Średnica: linia przechodząca przez środek, łącząca dwa punkty na obwodzie3
- Obwód: całkowita odległość wokół zewnętrznej krawędzi okręgu
Kluczowe relacje geometryczne
Zrozumienie połączeń między częściami okręgu jest kluczowe. Średnica jest zawsze dwa razy większa od promienia: d = 2r5.
Ta prosta zależność pomaga matematykom i inżynierom wykonywać precyzyjne obliczenia.
| Komponent okręgu | Definicja | Obliczenie |
|---|---|---|
| Promień | Odległość od środka do krawędzi | r = d/2 |
| Średnica | Najdłuższa linia przechodząca przez środek | d = 2r |
| Obwód | Odległość wokół okręgu | C = 2πr |
Znaczenie liczby Pi (π)
Pi to magiczna stała łącząca promień i obwód okręgu. Jej wartość około 3,14 jest kluczowa w obliczenia okręgu4.
Pi jest niezbędne do projektowania kół lub rozwiązywania łamigłówek geometrycznych. To liczba, której zawsze będziesz potrzebować.
π łączy pozornie prosty okrąg ze złożonymi zasadami matematycznymi3.
Opanowanie tych podstawowych elementów okręgu przygotowuje Cię do trudniejszych wyzwań geometrycznych3.
Wzór na obliczenie pola koła
Pomiary okręgu polegać na konkretnych wzorach do obliczeń. Te wzory są kluczowe do obliczenia pola koła. Zrozumienie właściwości okręgu ma kluczowe znaczenie dla dokładności obliczeń.
Obliczanie pola okręgu wykorzystuje wzory matematyczne oparte na promieniu lub średnicy. Przyjrzyjmy się krokom dokładnego obliczania pola okręgu.
Podział formuły obszaru
Główny wzór na pole koła jest prosty: A = πr²Oznacza to pomnożenie pi (π) przez promień do kwadratu6Oto co musisz wiedzieć:
- π wynosi około 3,14
- r oznacza promień okręgu
- Wzór działa na dowolny kształt okrągły
Metoda obliczeń krok po kroku
Aby obliczyć pole koła, wykonaj następujące kroki:
- Zmierz promień lub średnicę okręgu
- Jeśli używasz średnicy, podziel przez 2, aby uzyskać promień
- Podnieś promień do kwadratu
- Pomnóż przez π (3,14)
- Zaokrąglij do odpowiednich miejsc po przecinku
Praktyczne przykłady obliczania powierzchni
| Obiekt | Promień | Obliczanie powierzchni | Wynik |
|---|---|---|---|
| Koło rowerowe | 203 mm | π × (203)² | 129 737,85 mm² |
| Diabelski młyn | 60 metrów | π × (60)² | 11 309,73 m² |
„Opanowanie obliczeń powierzchni okręgu otwiera świat matematycznej precyzji i praktycznych zastosowań”. – Mathematical Insights
Regularne ćwiczenia pomogą Ci się wyróżnić pomiary okręguZ czasem nabędziesz wprawy w obliczeniach geometrycznych7.
Praktyczne zastosowania obliczeń pola koła
Geometria okręgu jest niezbędny w różnych branżach i zastosowaniach projektowych. Profesjonaliści używają go do rozwiązywania złożonych problemów i tworzenia innowacyjnych rozwiązań. Obliczenia okręgów pomóż nam zrozumieć, jaki wpływ mają okrągłe kształty na otaczający nas świat.
Zastosowania w przemyśle rzeczywistym
Obliczenia okręgów wykraczają poza prostą matematykę. Inżynierowie używają ich do projektowania systemów kół i przekładni. Systemy te redukują tarcie i umożliwiają wydajny transfer mocy.
Naukowcy wykorzystują pomiary kołowe do różnych celów. Szacują trajektorie, oceniają rozmiary planet i śledzą centra trzęsień ziemi.
Strategie projektowania i planowania
Obliczenia okręgów są kluczowe w projektach projektowych. Pomagają optymalizować przestrzeń i funkcjonalność w strukturach architektonicznych, takich jak kopuły. Pomiary powierzchni koła są również przydatne przy tworzeniu obwodów elektronicznych.
Architekci i inżynierowie polegają na precyzyjnych obliczeniach okręgów. Pomagają im one rozwijać stabilne konstrukcje i innowacyjne rozwiązania technologiczne.
Krytyczne rozważania dotyczące obliczeń
Aby uniknąć błędów, sprawdź dwukrotnie pomiary promienia. Weź również pod uwagę dokładną wartość pi. Pomiary okręgu mają wpływ na wiele obszarów, od technologii GPS po systemy obrazowania medycznego.
Opanowanie tych obliczeń jest potężne. Pozwala rozwiązywać złożone problemy przestrzenne w wielu dyscyplinach89.
Często zadawane pytania
Jaki jest podstawowy wzór na obliczenie pola koła?
Jak mogę obliczyć pole, jeśli znam tylko obwód koła?
Jakie jest znaczenie pi (π) w obliczeniach okręgu?
Jaka jest różnica między promieniem i średnicą?
Jakie są praktyczne zastosowania obliczeń pola koła?
Jakich typowych błędów należy unikać przy obliczaniu pól okręgów?
Jak dokonywać konwersji pomiędzy różnymi pomiarami okręgu?
Jakich jednostek należy użyć przy obliczaniu pola koła?
Linki źródłowe
- Jak znaleźć pole koła w 3 prostych krokach — Mashup Math – https://www.mashupmath.com/blog/how-to-find-the-area-of-a-circle
- Jak obliczyć pole koła • Alexander Math And Physics Tutoring – https://alexandertutoring.com/math-physics-resources/area-of-a-circle/
- Wszystko o okręgach: części okręgu, wzory i nie tylko – https://doodlelearning.com/maths/skills/shapes/circles
- Okręgi w matematyce – definicja, wzory, własności, przykłady – https://byjus.com/maths/circles/
- Pole koła – definicja, wzór, wyprowadzenie z rozwiązanymi przykładami – https://byjus.com/maths/area-of-circle/
- Kalkulator pola koła – https://www.omnicalculator.com/math/area-of-a-circle
- Pole koła | Wzór na promień, średnicę i obwód – https://tutors.com/lesson/area-of-a-circle
- Okręgi: Jakie są zastosowania okręgów w życiu codziennym? https://www.byjusfutureschool.com/blog/what-are-some-real-life-applications-of-circles/
- Zastosowania koła w życiu codziennym – GeeksforGeeks – https://www.geeksforgeeks.org/real-life-applications-of-circle/