How to Calculate Cumulative Frequency
Frequency analysis helps researchers understand data patterns in tanımlayıcı istatistikler. Cumulative frequency offers insights into data distribution and statistical trends1. It’s a key technique for making sense of complex datasets.
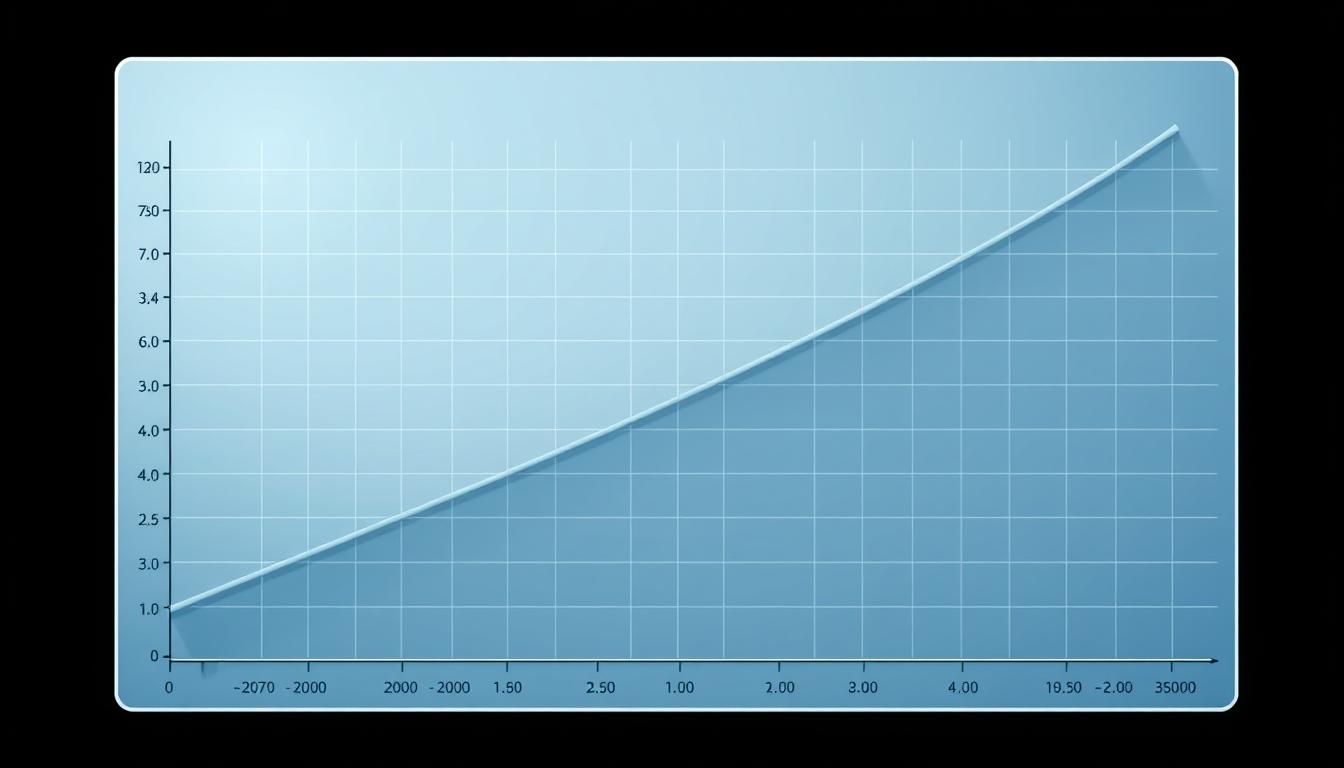
Cumulative frequency shows the running total of frequencies in a dataset. It tracks how data accumulates across different intervals2. This method helps analysts quickly grasp the total observations below a specific value3.
This concept is vital for veri görselleştirme and interpretation. It allows researchers to organize complex datasets effectively. As a result, statistical insights become more accessible and meaningful.
Önemli Noktalar
- Cumulative frequency tracks the total number of observations up to a specific point
- It is essential for tanımlayıcı istatistikler and data analysis
- Helps visualize data distribution and patterns
- Can be used across various research and academic disciplines
- Provides a comprehensive view of data accumulation
Understanding the Basics of Frequency Analysis
Statistical modeling relies on understanding data behavior. Probability distribution offers insights into variable organization and analysis. Every statistical study starts with grasping data’s key features.
Experts suggest using 5 to 20 classes for frequency distributions. This approach helps show data patterns clearly. It turns raw numbers into meaningful statistics.
Types of Variables in Statistical Analysis
Statistical analysis involves two main types of variables:
- Discrete Variables: Consist of separate, indivisible categories with no intermediate values
- Continuous Variables: Can be divided into infinite possible values
Importance of Data Organization
Good data organization is vital in statistical modeling. It helps researchers spot patterns and reduce errors. Proper arrangement also improves analytical accuracy.
Key Statistical Terms and Concepts
Grasping key statistical concepts leads to better analysis. Cumulative frequency shows the total frequencies across class intervals4. This method helps track data spread and spot important trends.
Data tells a story when organized and analyzed correctly.
How to Calculate Cumulative Frequency
Cumulative frequency is key in Data Mining Ve Exploratory Data Analysis. It tracks total observations below a specific value5. This method creates a running total of frequencies, revealing data distribution patterns3.
İle calculate cumulative frequency, şu adımları izleyin:
- Organize your raw data into a frequency distribution table
- Create a column for individual frequencies
- Calculate cumulative frequencies by adding each frequency to the previous total5
Formül basit: Cumulative Frequency = ∑ frequencies. In a summer camp dataset, the first age group’s frequency becomes its cumulative frequency.
The next group’s cumulative frequency adds its frequency to the previous total5.
| Gol | Sıklık | Cumulative Frequency | Relative Frequency |
|---|---|---|---|
| 45 | 1 | 1 | 0.071 (7.1%) |
| 50 | 2 | 3 | 0.143 (14.3%) |
| 55 | 3 | 6 | 0.214 (21.4%) |
Cumulative frequency graphs (ogives) help interpret these calculations visually. They show how the total grows across data points using cumulative frequency analysis.
The final cumulative frequency always equals the total number of observations3. This helps verify your calculations.
Çözüm
Calculating cumulative frequency is crucial in tanımlayıcı istatistikler. It helps researchers analyze complex datasets effectively. This skill allows for deep data interpretation and unlocks powerful insights6.
Arranging data from smallest to largest enables precise analysis. It helps in understanding distribution trends comprehensively6. Cumulative frequency methods make quantitative analysis more robust.
This technique helps identify medians and percentiles. It also reveals patterns within datasets6. Researchers can determine data point distributions efficiently.
Systematic frequency tracking reveals relationships between categorical variables7. The math behind cumulative frequency provides tools for statistical exploration. Formulas like relative cumulative frequency transform raw numbers into meaningful insights7.
These strategies enhance data interpretation significantly. They offer a comprehensive view of statistical distributions6. Practice calculating cumulative frequency with various datasets to improve your skills.
Each dataset tells a unique story. Careful analysis can uncover these hidden narratives. Cumulative frequency is a powerful tool in your analytical toolkit.
SSS
What exactly is cumulative frequency?
How is cumulative frequency different from regular frequency?
What’s the difference between calculating cumulative frequency for discrete and continuous variables?
Why is cumulative frequency important in data analysis?
How do I create a cumulative frequency graph (ogive)?
Can cumulative frequency be used in real-world applications?
What are some common challenges when calculating cumulative frequency?
How does cumulative frequency relate to other statistical techniques?
Kaynak Bağlantıları
- Cumulative Frequency – https://calcworkshop.com/exploring-data/cumulative-frequency/
- 10.06 Cumulative frequency tables and graphs | Year 11 Maths | NSW Mathematics Standard 11 – 2020 Edition – https://mathspace.co/textbooks/syllabuses/Syllabus-812/topics/Topic-18342/subtopics/Subtopic-246465/
- Cumulative vs Relative Frequency – GeeksforGeeks – https://www.geeksforgeeks.org/cumulative-vs-relative-frequency/
- Cumulative Frequency Distribution (Definition, Types and Graphs) – https://byjus.com/maths/cumulative-frequency-distribution/
- Cumulative Frequency, Percentiles and Quartiles – Wyzant Lessons – https://www.wyzant.com/resources/lessons/math/statistics_and_probability/averages/cumulative_frequency_percentiles_and_quartiles/
- Cumulative Frequency – (AP Statistics) – Vocab, Definition, Explanations | Fiveable – https://library.fiveable.me/key-terms/ap-stats/cumulative-frequency
- Cumulative frequency analysis – https://en.wikipedia.org/wiki/Cumulative_frequency_analysis
gelen kutusu üzerinden haberler
Nulla turp dis cursus. Tamsayı özgürlükleri euismod pretium faucibua