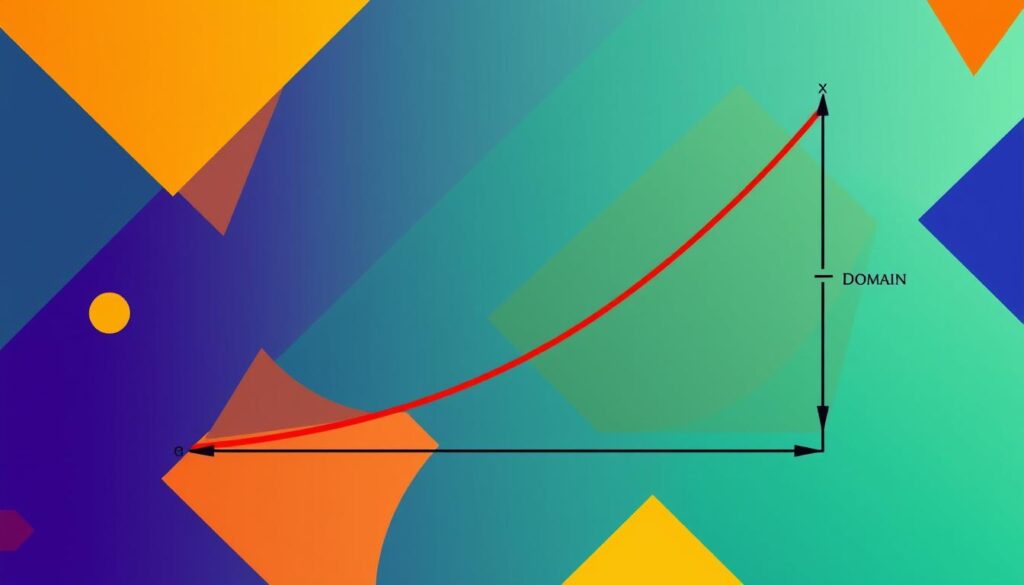
Domain and range are key concepts in mathematical functions. They help analyze how input values relate to output values. These ideas are vital for understanding mathematical relationships1.
Domain is the set of possible input values for a function. It’s the starting point for exploring math problems2. Domain determines which values can be used in a function1.
Range includes all potential output values from a function. It shows the results of mathematical transformations2. Knowing range helps predict how functions will behave.
Understanding domain and range improves function analysis skills. It allows for better prediction of mathematical outcomes. These concepts are fundamental to advanced math studies.
Key Takeaways
- Domain represents valid input values for functions
- Range shows all possible output values
- Mathematical functions have specific input restrictions
- Domain and range help predict function behavior
- Both concepts are essential in mathematical analysis
What is Domain in Mathematics?
The domain in math is all possible input values for a function. It’s like a collection of x-values that make a function work right. Understanding the domain set is key when exploring mathematical functions.
In math, the function domain acts as a gatekeeper. It decides which numbers can be valid inputs. Some functions have limits on their input values.
Understanding Domain Definition
A math domain includes all allowed input values where a function is defined. These values must meet certain conditions to produce meaningful outputs.
- Positive integers
- Real number ranges
- Specific numerical intervals
Practical Examples of Domain
Let’s look at some domain scenarios:
- For y = √(x + 4), the domain requires x ≥ -43
- Functions with square roots cannot have negative values under the radical
- Fractions cannot have zero in the denominator
Finding the Domain of a Function
To find a function’s domain, you need to:
- Identify potential input value restrictions
- Check for division by zero
- Ensure no negative values under square roots
- Examine logarithmic constraints
“The domain is your mathematical playground, defining where functions can dance and calculate.” – Math Enthusiast
Knowing input values helps you handle complex math functions with ease4. This knowledge is key to solving many math problems.
What is Range in Mathematics?
Range is vital in understanding mathematical functions. It’s the set of all possible output values a function can produce. Think of it as the endpoint for all inputs within a function’s domain.
Defining Mathematical Range
Mathematical range is the set of all possible outputs from a function’s domain. Mathematically speaking, each input might create a unique output. However, multiple domain values can lead to the same range value.
“The range reveals the potential destinations of a mathematical journey.” – Mathematical Insight
Examples of Function Range
- For the function x², the range set might include:
- Positive numbers
- Zero
- Non-negative real numbers
- A linear function could have a range spanning all real numbers
- Trigonometric functions have specific range limitations
Understanding Range Characteristics
Functions show unique range properties. The function x² with a domain of {−3, −2, −1, 1, 2, 3, 4} has a range of {1, 4, 9, 16}5.
Engineers and mathematicians use range analysis to understand system capabilities. It helps them grasp function behaviors in various fields6.
| Function Type | Typical Range Characteristics |
|---|---|
| Quadratic Functions | Non-negative real numbers |
| Linear Functions | All real numbers |
| Trigonometric Functions | Bounded intervals |
Studying function range offers deep insights into math relationships. It helps predict potential outputs across various fields6.
How to Determine Domain and Range
Domain and range calculation is key in function analysis. It helps in graphing functions and solving math problems. Knowing input and output values makes math easier7.
Mathematicians use two main methods for domain and range: graphical and analytical. These techniques offer unique insights into function behavior. They help in mathematical function analysis.
Graphical Method for Domain and Range
The graphical method involves looking at the function’s graph. You can spot restrictions and patterns quickly8.
- Observe horizontal axis for domain values
- Examine vertical axis for range values
- Look for any restrictions or breaks in the graph
Analytical Method for Function Analysis
The analytical method uses algebra and function properties. You’ll solve equations and find potential limits7.
| Function Type | Domain Characteristics | Range Characteristics |
|---|---|---|
| Linear Function | All real numbers | All real numbers |
| Square Root Function | Non-negative real numbers | Non-negative real numbers |
| Reciprocal Function | All real numbers except 0 | All real numbers except 0 |
Common Errors to Avoid
Watch out for these pitfalls in domain and range calculation:
- Forgetting division by zero restrictions
- Overlooking negative square root limitations
- Missing logarithmic function constraints
“In mathematics, precision is key. Always double-check your domain and range calculations.” – Mathematical Insight
Practice these methods to become skilled at graphing functions. You’ll analyze math relationships with confidence8.
Why Do Domain and Range Matter?
Domain and range are vital for mathematical modeling in many fields. They help define function limits and explore real-world situations. These concepts are key to analyzing functions and understanding their restrictions.
Domain and range are essential in data science and engineering. They’re used to predict growth, analyze trends, and design complex systems. Mathematical modeling relies on grasping function behaviors and their limits.
Understanding function limits helps solve complex problems in various areas. Different domain and range features can offer unique insights. Mastering these ideas boosts your analytical skills and problem-solving abilities.
By applying domain and range, you’ll tackle mathematical challenges with more confidence. These concepts open doors to deeper understanding in science and math. They’re powerful tools for exploring and explaining the world around us910.
FAQ
What exactly is the domain of a function?
How do I find the domain of a function?
What is the range of a function?
Why are domain and range important in real-world applications?
What’s the difference between domain and range?
Can a function have a restricted domain?
How can I represent domain and range?
Source Links
- Domain And Range Of A Functions – Domain and Range Meaning, Examples – https://byjus.com/maths/domain-codomain-range-functions/
- Domain and Range | How to Find Domain and Range of a Function – GeeksforGeeks – https://www.geeksforgeeks.org/domain-and-range-of-function/
- Domain and Range Practice Problems – https://www.intmath.com/functions-and-graphs/2a-domain-and-range.php
- Domain, Range and Codomain – https://www.mathsisfun.com/sets/domain-range-codomain.html
- What Is Range In Mathematics? – https://www.sciencing.com/what-range-mathematics-4865897/
- Domain and Range | Engineering Math Resource Center | College of Engineering – https://engineering.usu.edu/students/engineering-math-resource-center/topics/pre-calculus/algebra/domain-and-range
- Determine Domain and Range from a Graph – https://courses.lumenlearning.com/waymakercollegealgebra/chapter/find-domain-and-range-from-a-graph/
- Determining the Domain and Range for Linear Functions – https://texasgateway.org/resource/determining-domain-and-range-linear-functions
- 17.2.3: Finding Domain and Range – https://math.libretexts.org/Bookshelves/Applied_Mathematics/Developmental_Math_(NROC)/17:_Functions/17.02:_Using_Functions/17.2.03:_Finding_Domain_and_Range
- PDF – https://caps.unm.edu/mathrefresh/assets/DomainsandRanges.pdf